Skip to contents

Simulation-based Calibration

Niek Stevenson

Source: vignettes/Simulation-based-Calibration.Rmd
Simulation-based-Calibration.Rmd

Introduction

Simulation-based calibration(SBC) is a technique used to validate and calibrate Bayesian estimation methods and models (Talts et al. 2018). SBC checks whether a model correctly accounts for uncertainty and whether the posterior distributions it produces are consistent with the true data-generating process. First we outline how to perform SBC in theory, after which we describe our experiences with SBC in EMC2, which will also illustrate how to perform SBC for your own model.

How to SBC

Here we briefly outline the steps to performing SBC, for more detail we refer the reader to Talts et al. (2018).

1. Specify the Probabilistic Model

  • Define the Bayesian model you’re working with. This includes specifying the prior distribution for the parameters and the likelihood function that connects the data to the parameters.
  • For example, suppose you have a model with a set of parameters α\alpha and observed data yy such that y∼p(y|α)y \sim p(y|\alpha) and α∼p(α)\alpha \sim p(\alpha).

2. Simulate Parameters and Data

  • Sample Parameters: Draw a large number of sets of parameters α(i)\alpha^{(i)} from the prior distribution p(α)p(\alpha).
  • Simulate Data: For each set of set parameters α(i)\alpha^{(i)}, simulate a dataset y(i)y^{(i)} from the likelihood p(y|α(i))p(y|\alpha^{(i)}).

3. Compute Posterior Distributions

  • For each simulated dataset y(i)y^{(i)}, compute the posterior distribution p(α|y(i))p(\alpha | y^{(i)}) using your Bayesian model.

4. Evaluate the Rank Statistics

  • For each simulated dataset, determine where the set of true parameters α(i)\alpha^{(i)} ranks in the posterior samples of α\alpha. In EMC2 we thin the posterior to be equal to the effective sample size. The rank is essentially the number of posterior samples that are less than the true α(i)\alpha^{(i)}.
  • Normalize the ranks to lie between 0 and 1. This is your rank statistic.

5. Check Uniformity

  • Aggregate the rank statistics across all simulated data-sets. If your model is well-calibrated, the ranks should be uniformly distributed because each posterior should correctly reflect the uncertainty about the parameter.
  • Plot the rank statistics. Here we present both histograms of the rank statistic and plot that compares the empirical cumulative rank to the cumulative density function of a uniform distribution.

Non-hierarchical SBC in EMC2

EMC2 allows for both hierarchical and non-hierarchical estimation. Given the desirable statistical and estimation properties of hierarchical models, we normally recommend to use hierarchical models. However, given that estimating hundreds of models is quite time consuming and practically unfeasible without a computational server, we recommend running SBC on non-hierarchical models for typical applications. Here we use the LBA and DDM to illustrate non-hierarchical SBC. Later we’ll also perform hierarchical SBC for the LBA, DDM, RDM and LNR. First we clear our workspace and load EMC2

rm(list = ls())
library(EMC2)

Compression

Before we start with the SBC, we want to give a quick note on data compression. By default EMC2 compresses RTs to bins of 20ms, since typical lab set-ups do not allow response times to be measured with a higher resolution. However, generated data is not subject to the same physical constraints. Therefore, and to avoid biases, compression is turned off. To turn on compression regardless, you can set compression = TRUE, and set the resolution using rt_resolution = 0.02 (for example) in the run_sbc function, which will speed up computation but potentially introduces biases.

LBA

To run SBC we specify a design and a prior for the model. EMC2 assumes normal priors on the parameters for non-hierarchical models. Thus, some parameters are transformed to better match the normal prior and to satisfy the assumption of the normal distribution to have full support on the real line. To check the parameter transformations we use ?LBA .

matchfun <- function(d) d$S == d$lR

design_LBA <- design(factors=list(subjects=1,S=c("left", "right")),
                     Rlevels = c("left", "right"),
                     matchfun = matchfun,
                     formula =list(v~lM,B~1, t0~1, sv~1, A~1),
                     constants=c(sv=log(1)),
                     model = LBA)

prior_LBA <- prior(design_LBA, type = "single",
                  pmean = c(1.3, .7, log(.8), log(.2), log(.3)),
                  psd = c(.2, .1, .1, .05, .05))

Now we plot the prior, with map = TRUE (the default) to see the implied prior on the transformed parameters.

plot_prior(prior_LBA, design_LBA)

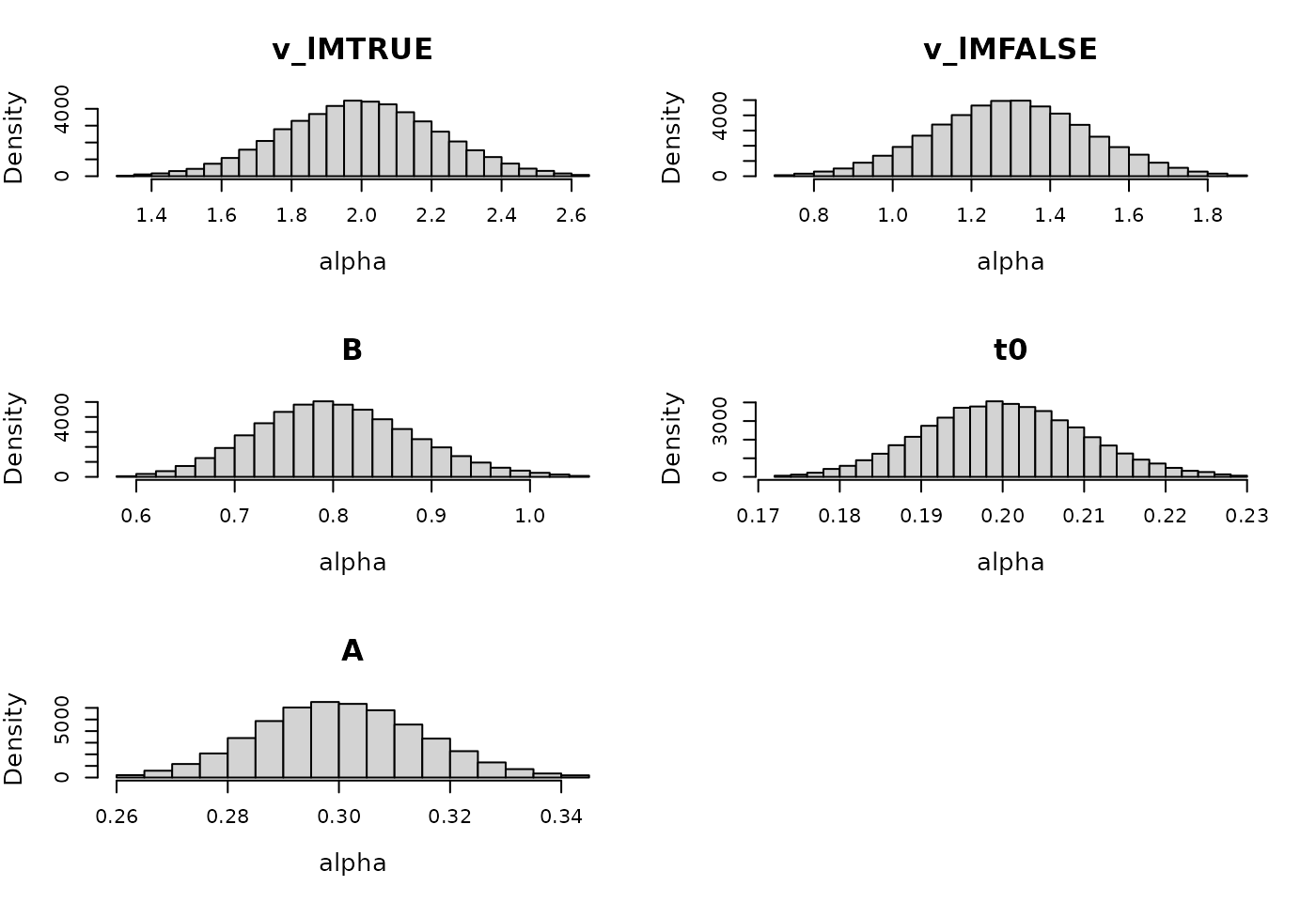
Prior for LBA non-hierarchical model

Next we can simply call run_sbc with our specified design and prior. We can use ?run_sbc to see the description of the function arguments. The trials argument refers to the number of trials per cell. Since we have an 2-level S factor in our design (and all other designs used), we will thus simulate 200 trials per data set. Also note that by default run_sbc will estimate till the point-scale reduction factor is smaller than 1.1 and the minimum effective sample size of any of the estimated parameters is larger than 100.

SBC_LBA_single <- run_sbc(design_LBA, prior_LBA, replicates = 500, trials = 100, plot_data = FALSE,
                  iter = 1000, n_post = 1000, fileName = "SBC_data/SBC_LBA_single.RData",
                  cores_per_chain = 30)

In non-hierarchical models, setting cores_per_chain = 30 will estimate 30 simulated data-sets simultaneously. Which is feasible on the computational server we used. But given that the LBA is so quick to compute, non-hierarchical SBC is also feasible on a personal computer. It is recommended to specify fileName to store intermediary results in case of crashes.

EMC2 also comes with plotting functions that allow us to visualize the results. First we can plot the standard histograms, with a number of equally spaced bins between 0 and 1 of the normalized rank statistic.

plot_sbc_hist(SBC_LBA_single, bins = 10)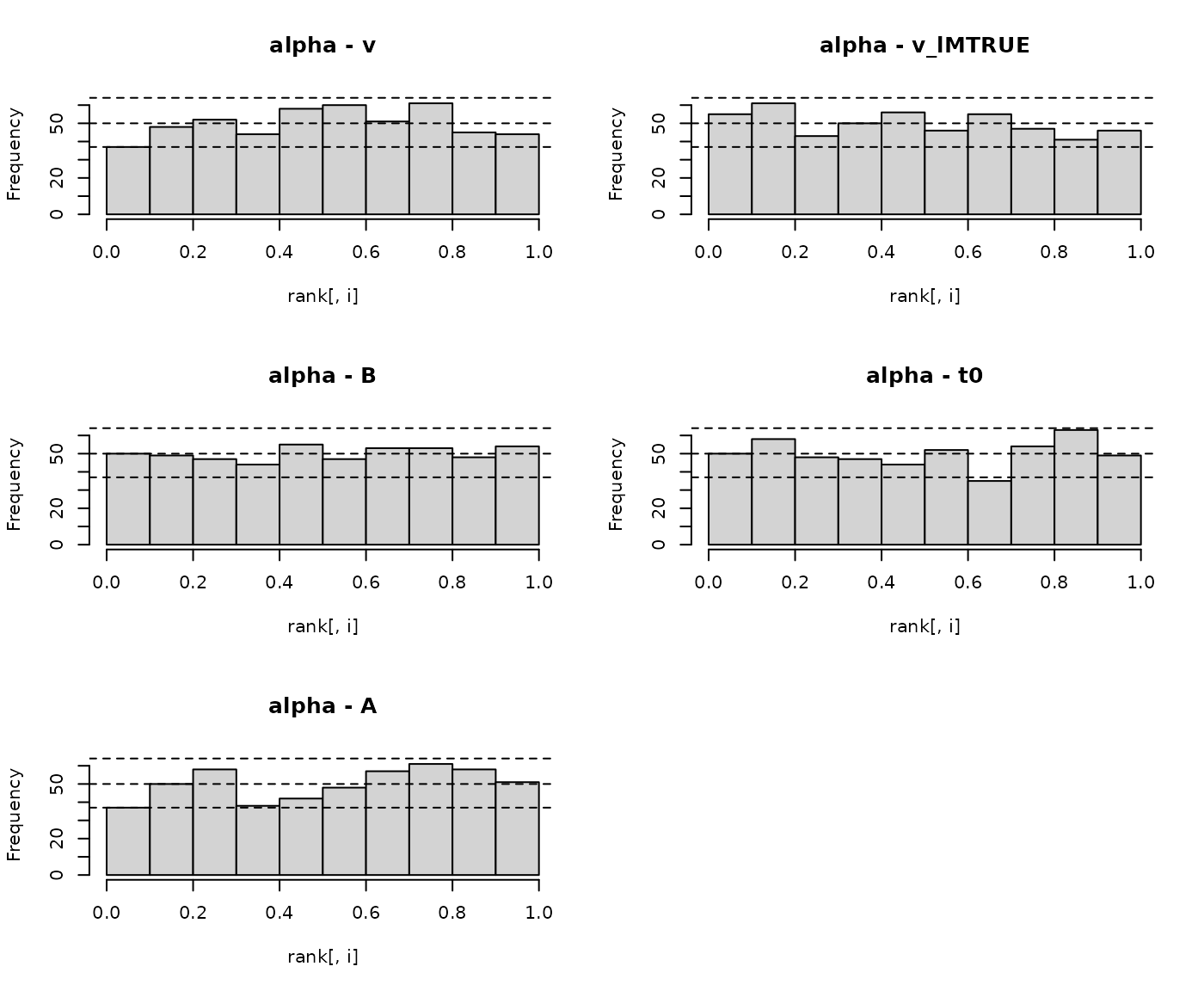

Histogram SBC LBA single

Here the gray lines indicate the 2.5, 50 and 97.5% percentile of where n samples from a uniform distribution are expected to fall. As we can see most of the bins are are nicely within these bounds and no clear pattern emerges. However, this visualization very much depends on bin size, as pointed out by Talts et al. (2018). Therefore EMC also comes with plots that visualize the difference in the empirical cumulative density function (ecdf) and the cumulative density function of a uniform distribution.

plot_sbc_ecdf(SBC_LBA_single)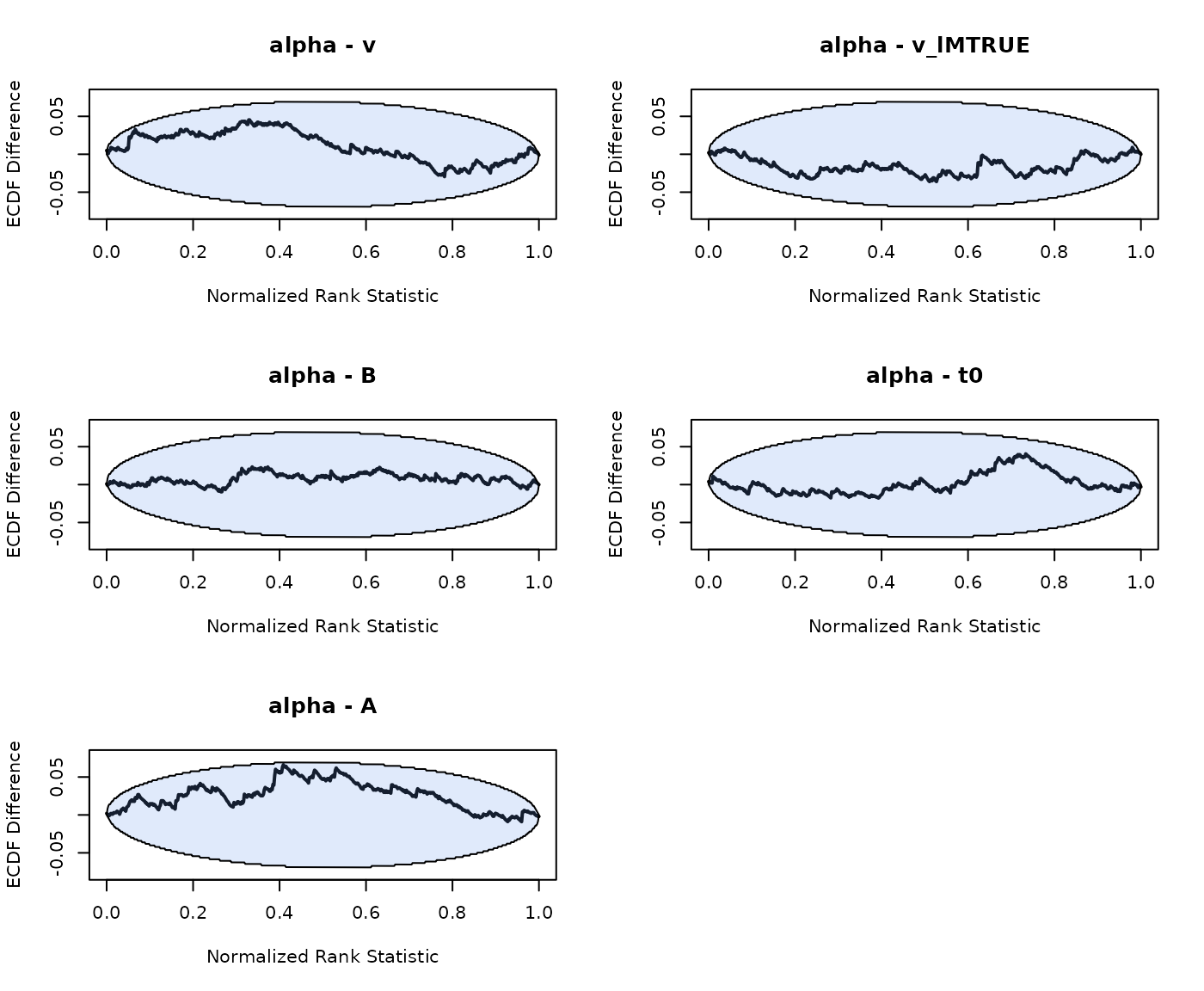

ecdf LBA single

In these dinosaur eggs the blue area visualizes the 95% area of expected cumulative values. As with real eggs, the observed line, (i.e. the cracks) should obviously lie somewhere on the egg. For an explanation and guide to interpretation to these plots we recommend the following article https://hyunjimoon.github.io/SBC/articles/rank_visualizations.html. In the remainder of this article we’ll use these plots to visualize SBC results.

DDM

Next we test non-hierarchical for the DDM as well. Initial results actually showed bias in the estimation of non-decision time and non-decision time variability. Whereas we first based our DDM implementation on the rtdists package (Singmann et al. 2022), the bias pushed us to test with alternative packages, after which we stumbled on the WienR package (Hartmann and Klauer 2023). Which not only boasts faster likelihood evaluations, but also no longer shows bias in the SBC results. Hence in the newest CRAN release we adapted our C++ code to instead use the WienR C++ routines.

For the SBC itself we used the following prior and design settings, again being mindful of the required transformations.

#?DDM
design_DDM <- design(factors=list(subjects=1,S=c("left", "right")),
                       Rlevels = c("left", "right"),
                       formula =list(v~1,a~1, t0~1, s~1, Z~1, sv~1, SZ~1, st0 ~ 1),
                       constants=c(s=log(1)),
                       model = DDM)


prior_DDM <- prior(design_DDM, type = "single",
                  pmean = c(1, log(.8), log(.3), qnorm(.5), log(.1), qnorm(.05), log(.05)),
                  psd = c(.15, .15, .1, .05, .15, .15, .15))

SBC_DDM_single <- run_sbc(design_DDM, prior_DDM, replicates = 500, trials = 100, 
                          fileName = "SBC_data/SBC_DDM_single.RData", cores_per_chain = 30)

Next we plot the ECDF difference plot again.

plot_sbc_ecdf(SBC_DDM_single)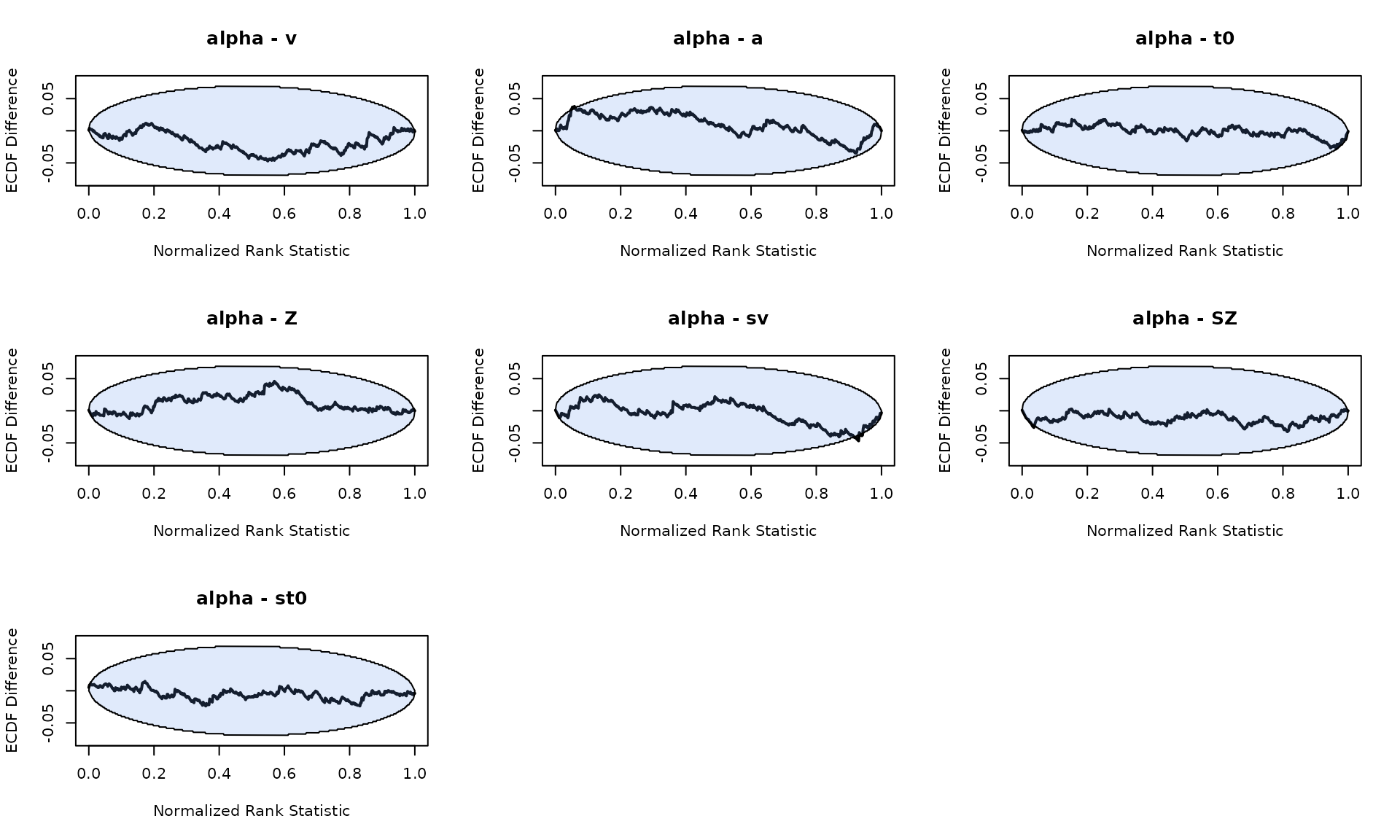

ecdf DDM single

As you can see minor misfits in a and sv but nothing too worrying. To double check we did refits, that showed that this bias is not systematic.

Hierarchical SBC

Besides being a friendly introduction to doing SBC in EMC2, this post also serves as a test of unbiased estimation of the four main classes of EAMs included in EMC2. Still we would recommend the user to typically run SBC on non-hierarchical models, except when doing model development.

The approach to running hierarchical SBC is very similar to running non-hierarchical SBC. However we can now write the model of data yy as y∼p(y|α)p(α|θ)p(θ)y \sim p(y|\alpha)p(\alpha|\theta)p(\theta). Here p(θ)p(\theta) is the prior on the group-level parameters. The generated data for one sample y(i)y^{(i)} is still generated from α(i)\alpha^{(i)}, but with α(i)\alpha^{(i)} generated from θ(i)\theta^{(i)}, with θ(i)∼p(θ)\theta^{(i)} \sim p(\theta).

Prior structure

Although in the paper we rely on the prior structure defined by Huang and Wand (2013), which is also the default in EMC2, this prior structure has a lot of mass near zero for the group-level variance parameters (a half-t distribution). From a Bayesian posterior view these prior structures are attractive (Gelman 2006), since they do not artificially increase the variance estimates and thus err on the safe side. However, in SBC data-generation this means we sample many data-sets with no individual differences. Unfortunately, for numerical reasons EMC2 cannot recover a true zero on group-level variances. Thus, EMC2 will both have difficulty converging and it will identify, albeit very small, some degree of individual differences. Therefore, the type = "standard" prior structure results in biased SBC variance estimates. Therefore, in SBC we recommend using type = "diagonal-gamma", which as the name suggests uses gamma distributions for the variance parameters, which have less mass at zero.

Nevertheless we believe the standard prior is not problematic in real data, since it will always contain at least some degree of individual differences (only a true zero cannot be recovered).

LBA

Now we dive into hierarchical SBC for the LBA model. The prior structure we chose was as follows. Here we have to be extra mindful of choosing a prior that ensures plausible generated data, since there’s a double propagation of induced variance through the prior. First through the prior on the standard deviation of the group-level mean, but also through the prior on the group-level variance.

n_subjects <- 30
# 
matchfun <- function(d) d$S == d$lR

design_LBA <- design(factors=list(subjects=1:n_subjects,S=c("left", "right")),
                     Rlevels = c("left", "right"),
                     matchfun = matchfun,
                     formula =list(v~lM,B~1, t0~1, sv~1, A~1),
                     constants=c(sv=log(1)),
                     model = LBA)

prior_LBA <- prior(design_LBA, type = "diagonal-gamma",
                  mu_mean = c(1.3, .7, log(.8), log(.2), log(.3)),
                  mu_sd = c(.2, .1, .1, .05, .05),
                  shape = 10,
                  rate = c(.2, .2, .2, .1, .1))

We can also plot what the implied prior range is of the subject-level parameters:

plot_prior(prior_LBA, design_LBA, selection = "alpha")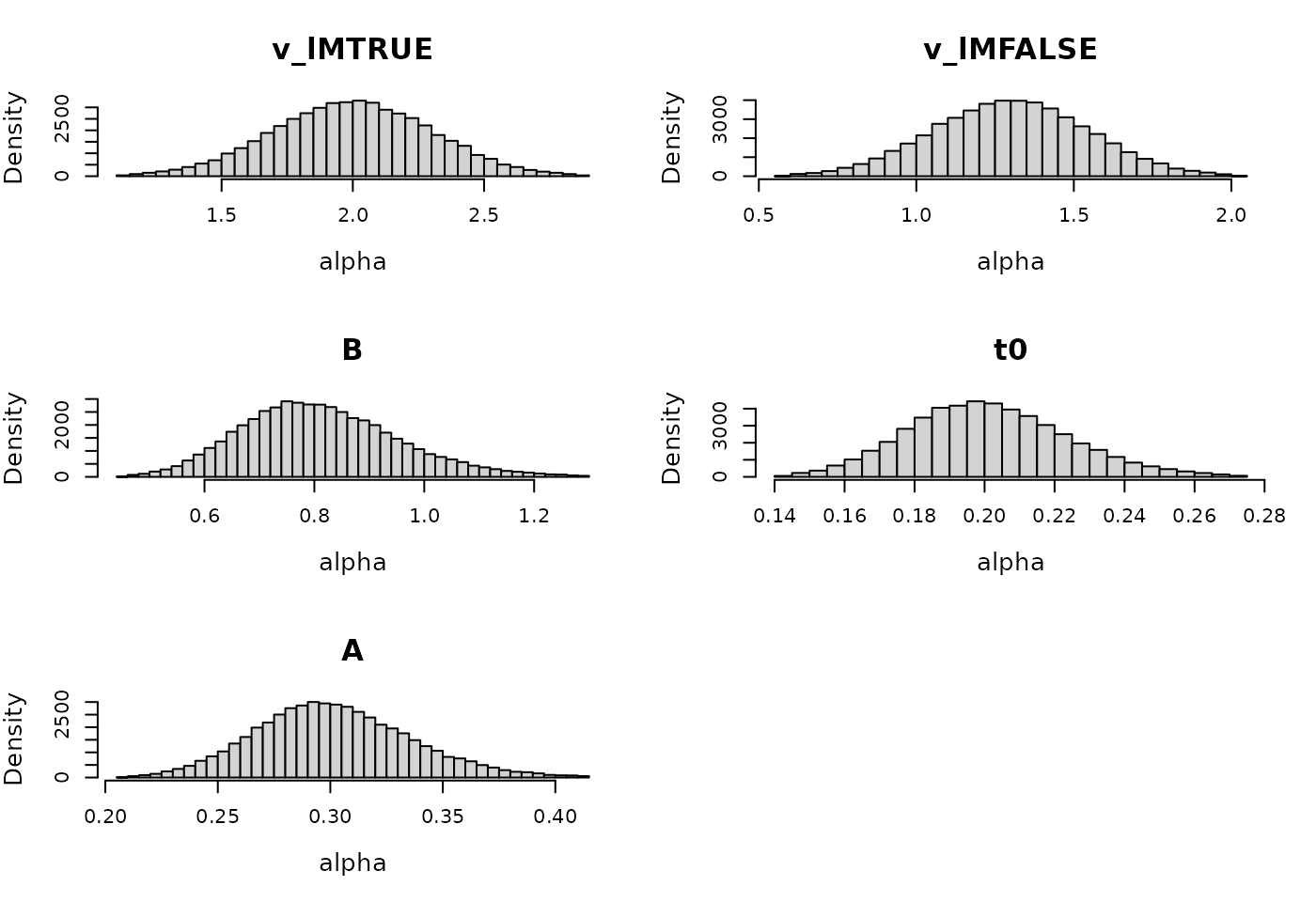

Prior for LBA hierarchical model

To actually run SBC, we can use the same function as before, now also specifying how many subjects we want to have in the hierarchical model

SBC_LBA <- run_sbc(design_LBA, prior_LBA, replicates = 500, trials = 100,
                        n_subjects = n_subjects, fileName = "SBC_data/SBC_LBA.RData", cores_per_chain = 30)

We can also plot the results again using the plot_sbc_ecdf function. It will now generate a set of ECDF difference plots for the hierarchical variance ranks and the hierarchical means ranks:

plot_sbc_ecdf(SBC_LBA)

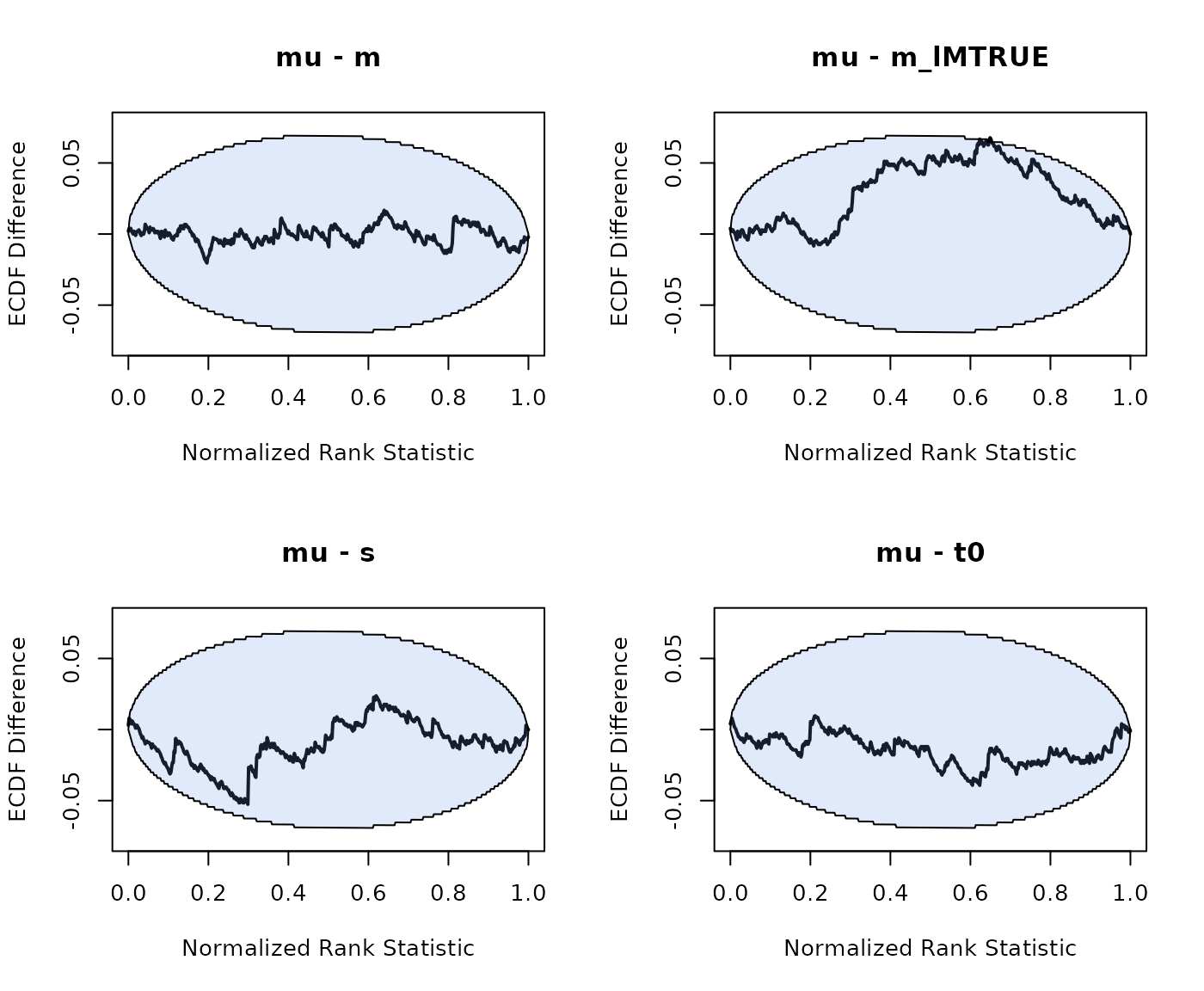
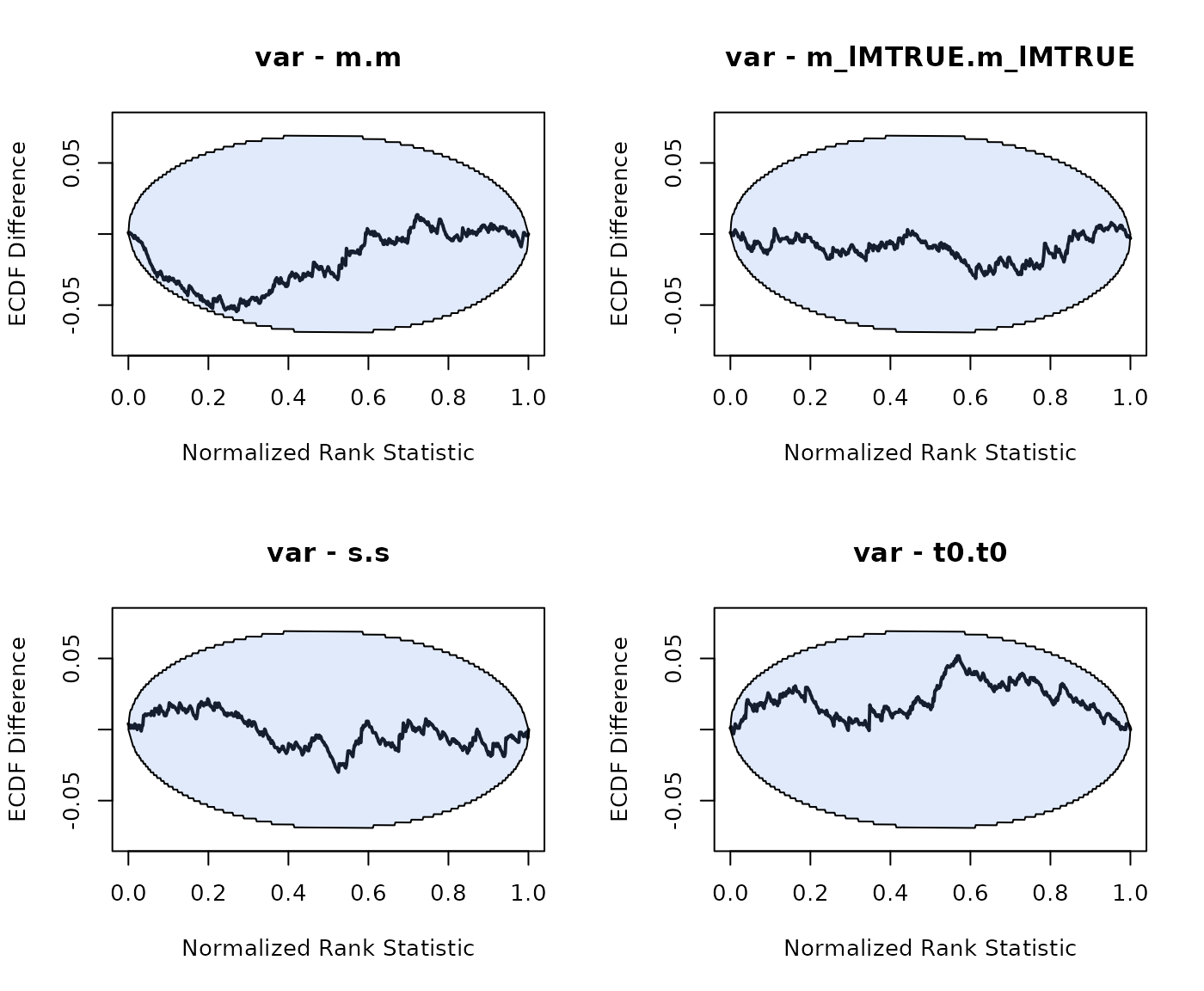
ECDF SBC LBAECDF SBC LBA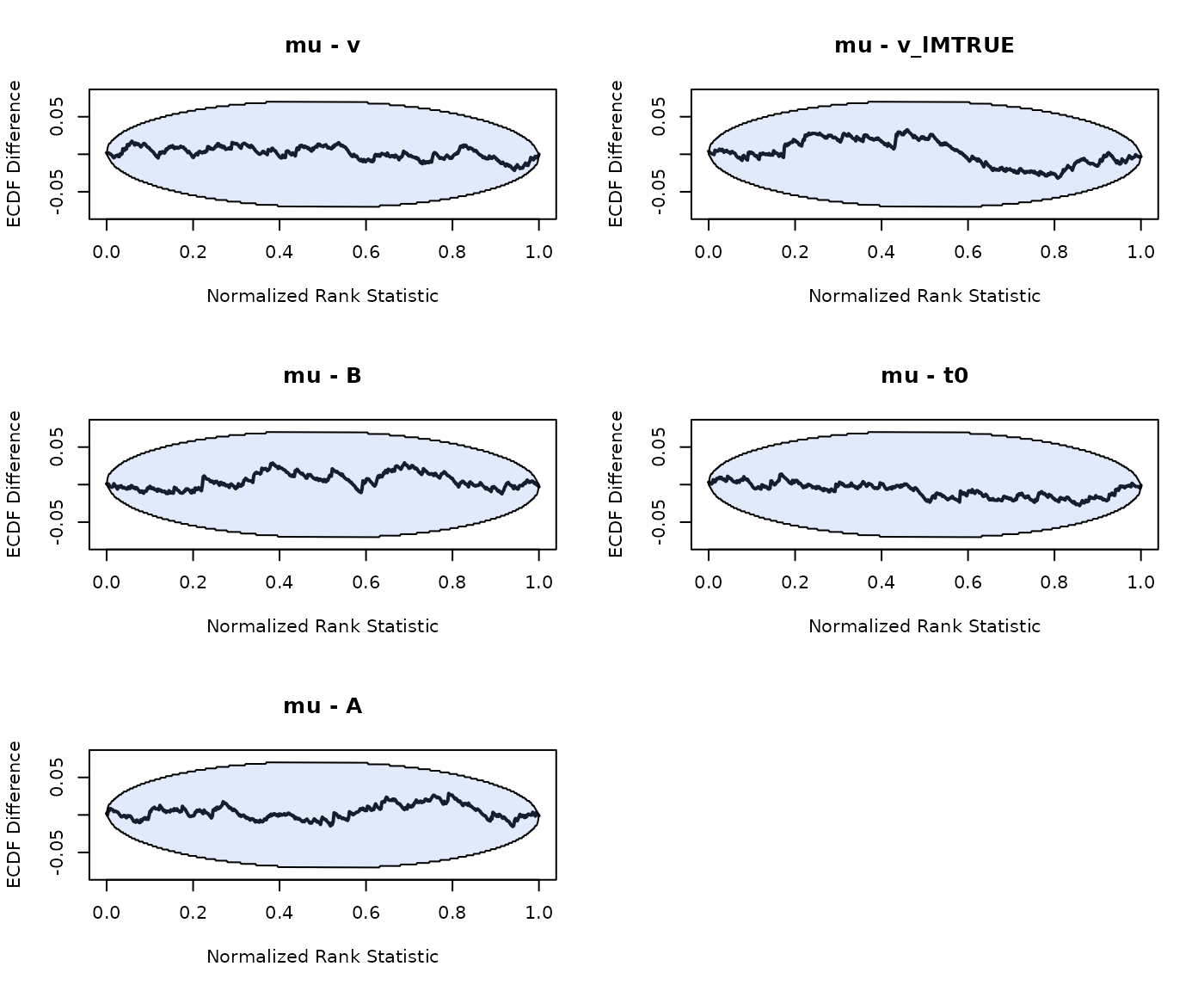

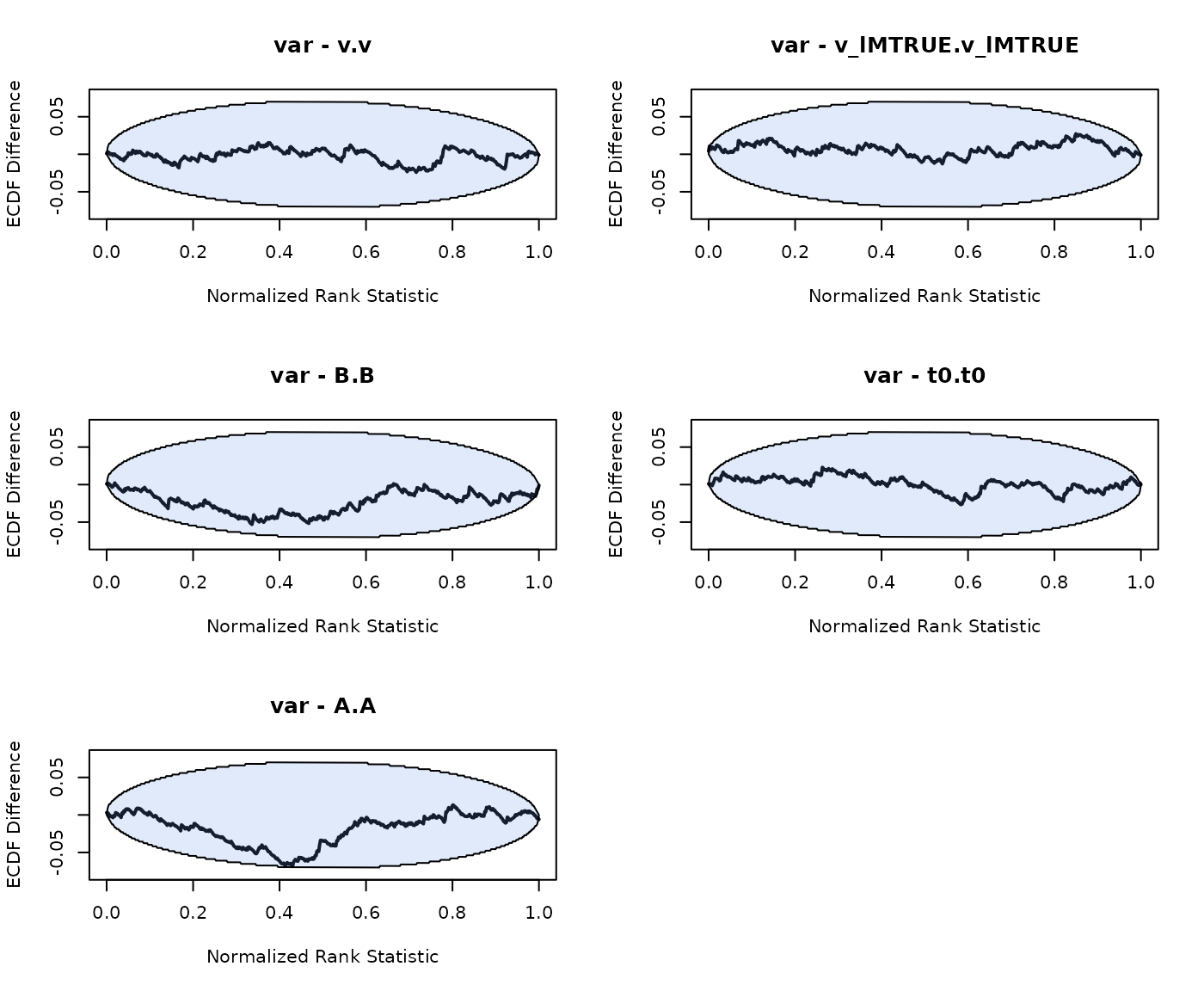
As we can see good results for the hierarchical SBC and no noticable bias in the group-level mean or variance parameters.

DDM

We also tested hierarchical SBC for the seven parameter DDM. We again chose priors carefully here to match realistic behavioral data.

n_subjects <- 30

design_DDM <- design(factors=list(subjects=1:n_subjects,S=c("left", "right")),
                       Rlevels = c("left", "right"),
                       formula =list(v~1,a~1, t0~1, s~1, Z~1, sv~1, SZ~1, st0 ~ 1),
                       constants=c(s=log(1)),
                       model = DDM)


prior_DDM <- prior(design_DDM, type = "diagonal-gamma",
                  pmean = c(1.2, log(.8), log(.3), qnorm(.5), log(.1), qnorm(.05), log(.05)),
                  psd = c(.15, .15, .1, .05, .1, .1, .15),
                  shape = 10,
                  rate = c(.2, .2, .2, .1, .1, .1, .1))

In contrast to the other models, we generated 200 (instead of 100) trials per person per cell, since with 100 trials the model sometimes did not converge or was very slow to converge. We also only generated 250 data sets due to the large computational costs associated with running a full hierarchical DDM.

SBC_DDM <- run_sbc(design_DDM, prior_DDM, replicates = 250, trials = 200,
                        n_subjects = n_subjects, fileName = "SBC_data/SBC_DDM.RData", cores_per_chain = 30)

The group-level means look unbiased, the group-level variance of the between trial variability parameters is overestimated a bit. We note that the effective sample size for these parameters is also very small (although minimum a 100), which can bias the results (Talts et al. 2018).

plot_sbc_ecdf(SBC_DDM)

ECDF SBC DDMECDF SBC DDM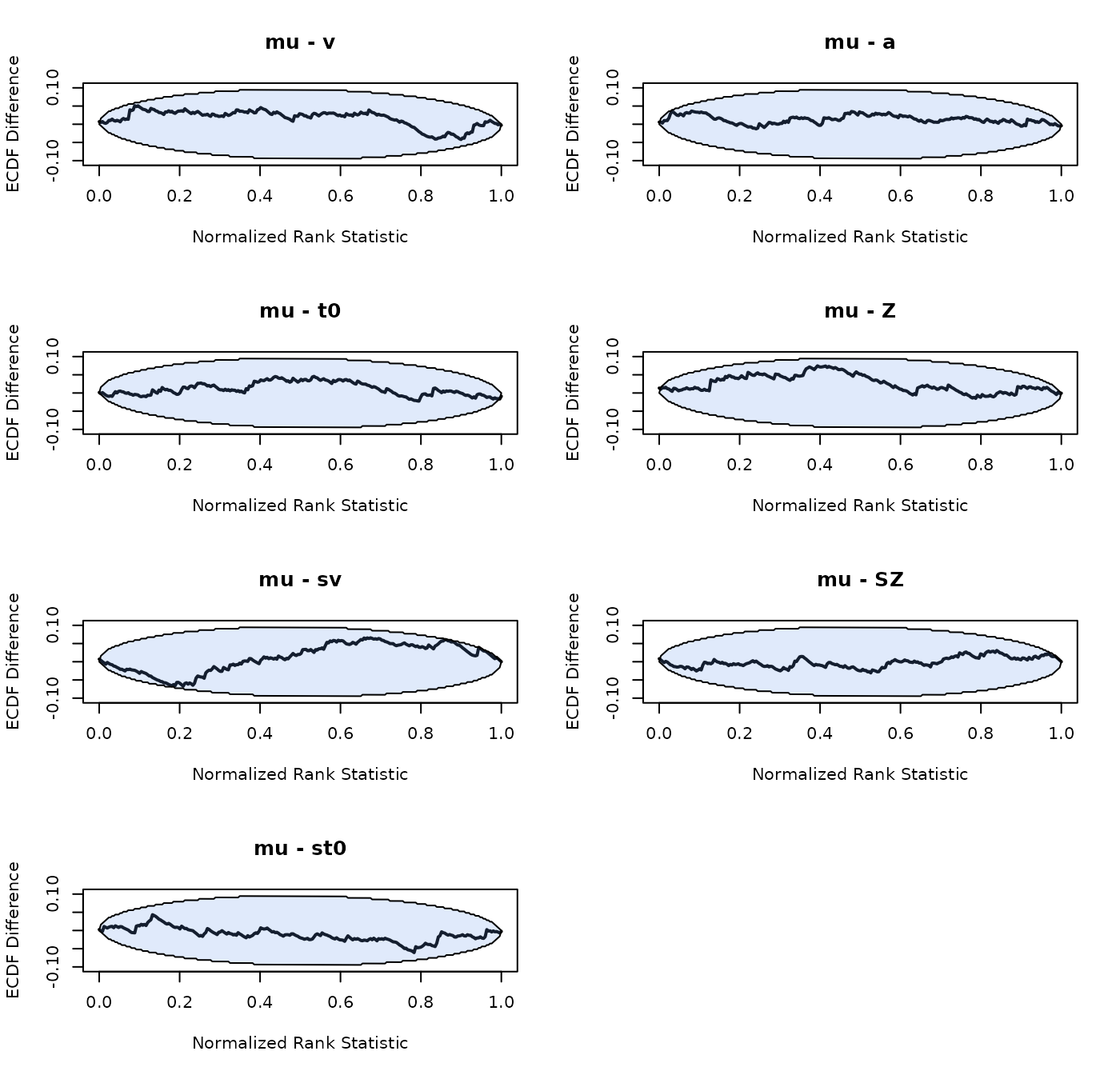

RDM

For completeness and as a proof of correct implementation we also test hierarchical SBC for the RDM with the following model definition and prior structure.

n_subjects <- 30

matchfun <- function(d) d$S == d$lR


design_RDM <- design(factors=list(subjects=1:n_subjects,S=c("left", "right")),
                     Rlevels = c("left", "right"),
                     matchfun = matchfun,
                     formula =list(v~lM,B~1, t0~1, A~1, s ~ 1),
                     constants=c(s=log(1)),
                     model = RDM)

prior_RDM <- prior(design_RDM, type = "diagonal-gamma",
                  mu_mean = c(1.4, .3, log(1.5), log(.2), log(.3)),
                  mu_sd = c(.05, .1, .1, .05, .05),
                  shape = 10,
                  rate = c(.1, .2, .2, .2, .1))

SBC_RDM <- run_sbc(design_RDM, prior_RDM, replicates = 500, trials = 100,
                        n_subjects = n_subjects, fileName = "SBC_RDM.RData", cores_per_chain = 30)

We again note that SBC shows no bias in the hierarchical RDM model:

plot_sbc_ecdf(SBC_RDM)

ECDF SBC RDMECDF SBC RDM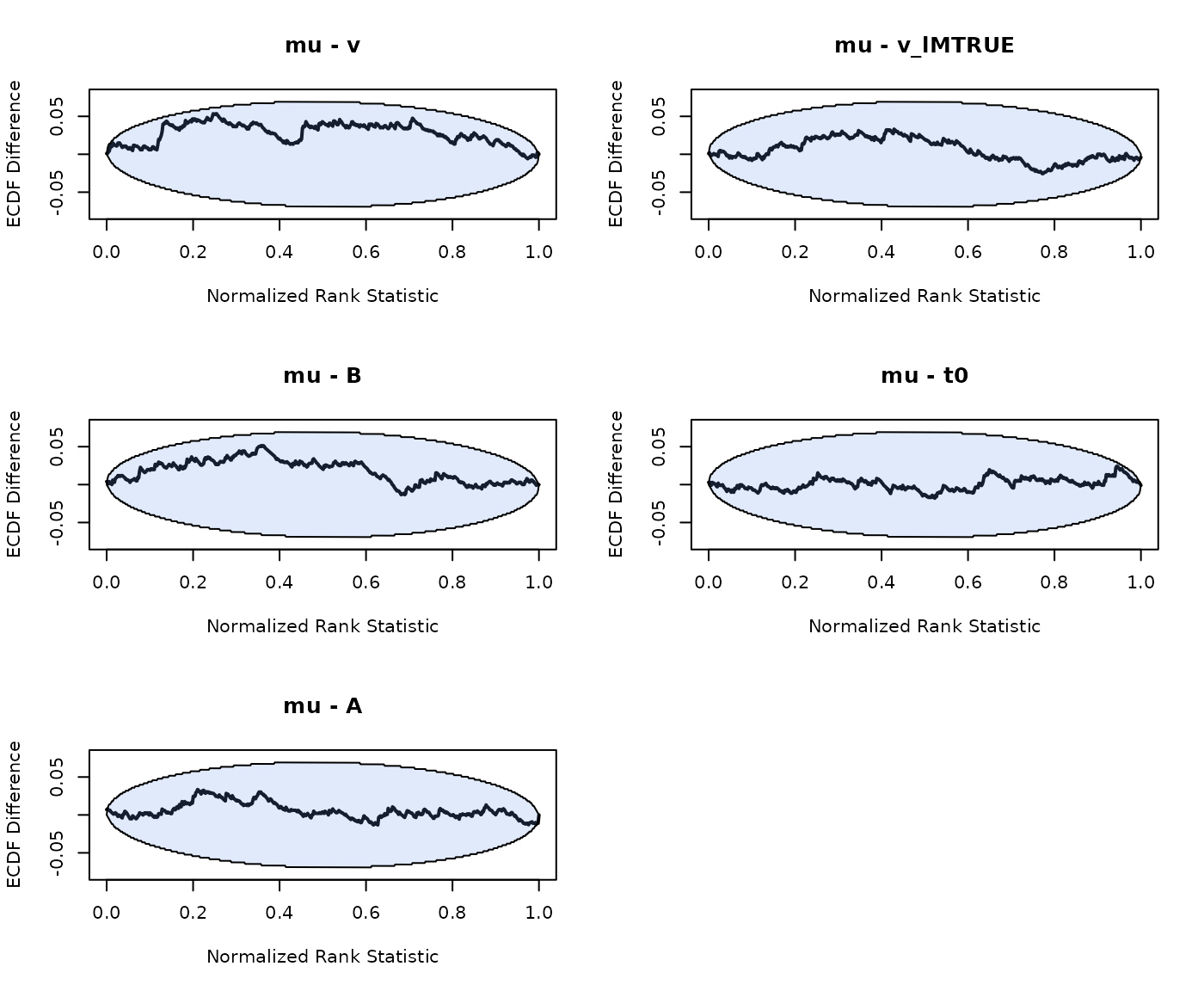

LNR

Lastly, we run hierarchical SBC for the LNR with the following specification

n_subjects <- 30

matchfun <- function(d) d$S == d$lR

design_LNR <- design(factors=list(subjects=1:n_subjects,S=c("left", "right")),
                     Rlevels = c("left", "right"),
                     matchfun = matchfun,
                     formula =list(m~lM,s~1, t0~1),
                     model = LNR)

prior_LNR <- prior(design_LNR, type = "diagonal-gamma",
                  mu_mean = c(-.7, -.5, log(1), log(.2)),
                  mu_sd = c(.2, .1, .1, .05),
                  shape = 10,
                  rate = c(.2, .2, .2, .1))

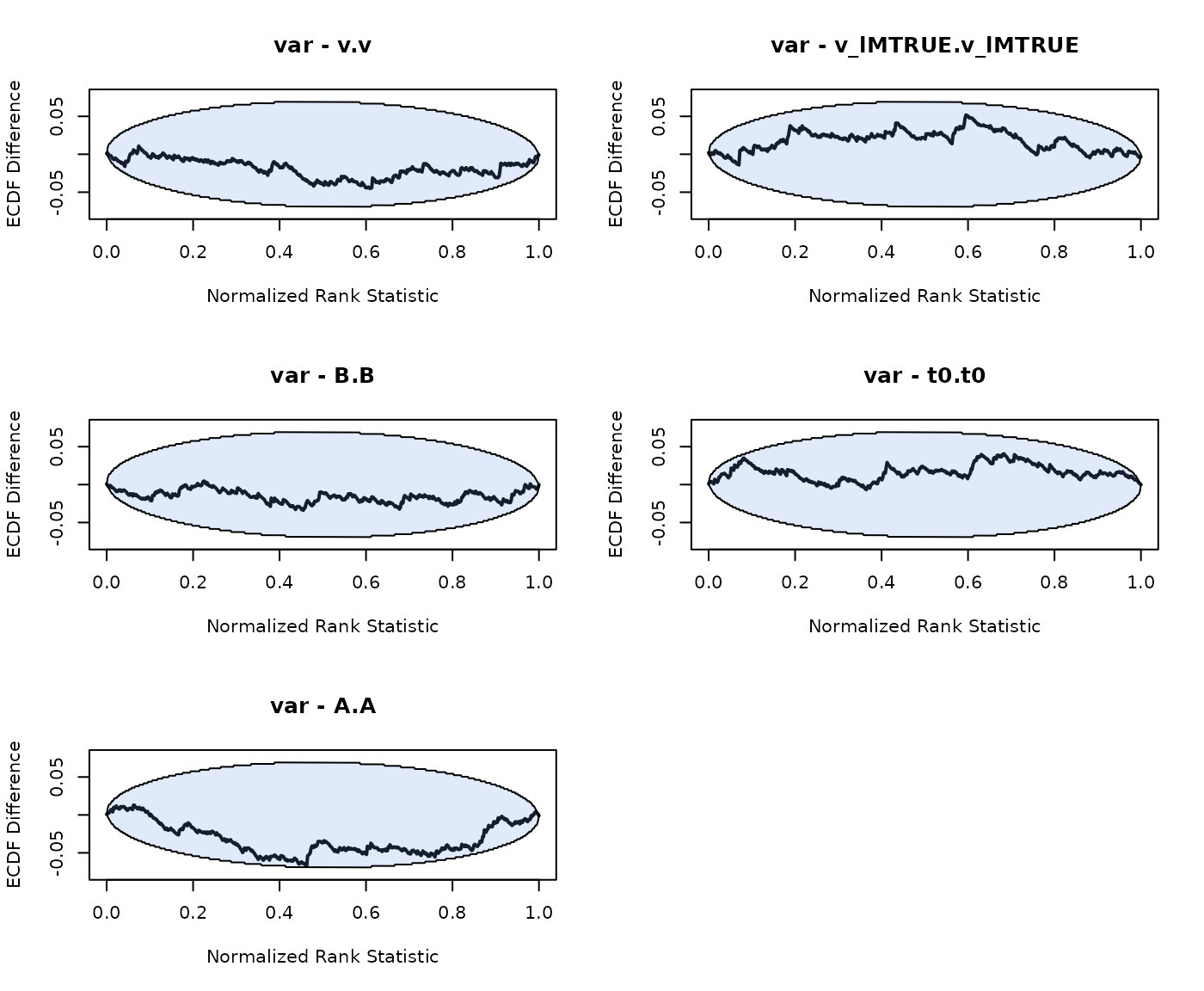
SBC_LNR <- run_sbc(design_LNR, prior_LNR, replicates = 500, trials = 100,
                        n_subjects = n_subjects, fileName = "SBC_LNR.RData", cores_per_chain = 30)

For the LNR hierarchical SBC also shows no considerable bias:

plot_sbc_ecdf(SBC_LNR, layout = c(2,2))

ECDF SBC RDMECDF SBC RDM

Gelman, Andrew. 2006. “Prior distributions for variance parameters in hierarchical models (comment on article by Browne and Draper).” Bayesian Analysis 1 (3): 515–34. https://doi.org/10.1214/06-BA117A.
Hartmann, Raphael, and Karl C. Klauer. 2023. WienR: Derivatives of the First-Passage Time Density and Cumulative Distribution Function, and Random Sampling from the (Truncated) First-Passage Time Distribution. https://CRAN.R-project.org/package=WienR.
Huang, Alan, and M. P. Wand. 2013. “Simple Marginally Noninformative Prior Distributions for Covariance Matrices.” Bayesian Analysis 8 (2): 439–52. https://doi.org/10.1214/13-BA815.
Singmann, Henrik, Scott Brown, Matthew Gretton, and Andrew Heathcote. 2022. Rtdists: Response Time Distributions. https://CRAN.R-project.org/package=rtdists.
Talts, Sean, Michael Betancourt, Daniel Simpson, Aki Vehtari, and Andrew Gelman. 2018. “Validating Bayesian Inference Algorithms with Simulation-Based Calibration.” arXiv Preprint arXiv:1804.06788.